ORIGINAL SOURCE: http://www.cs.cmu.edu/~bryant/boolean/maps.html

Интересни проблеми со мапи

Дон Кнут работи на том 4 од Уметност на компјутерско програмирање. Едно од поглавјата е на Дијаграмите за бинарни одлуки и нивните апликации, предмет за кој сметам дека е многу интересен. Кнут покажува дека најразлични интересни проблеми со графиконите можат да се кодираат како формули во Булија, а изведениот БДД ги претставува сите можни решенија за проблемот. Честопати постои некаков критериум за оптимизација и прилично е лесно да се извлече „најдоброто“ решение од БДД со едноставен динамичен алгоритам за програмирање..

Еве неколку примери, користејќи го графикот што ги претставува 48 соседни состојби, со јазол за секоја држава и предност помеѓу две држави ако споделат граница. За секоја од мапите, ако кликнете на неговата слика, ќе стигнете до изворниот документ SVG формат. Еве го графиконот, лоцирајќи ги јазлите во главните градови на државите:

Капитал тури

Да претпоставиме дека сакате да го посетите 48 државниот капитал со услов да поминувате низ секоја држава само еднаш. (Со други зборови, сакате да пронајдете Хамилтонска патека во графиконот.) Како што можете да видите од горенаведената карта, доколку ја следите најдиректната рута помеѓу државните метрополи, честопати ќе поминувате низ друга држава, или во случај на одејќи од Лансинг, Мичиген до Медисон, Висконсин, ќе возите преку езерото Мичиген. Наместо тоа, треба да ја преземете најкратката патека за возење што останува во рамките на двете држави за секој дел од патувањето. Дозволете ни да ја наречеме таква рута капитална турнеја. Еве еден дијаграм на дозволените патеки меѓу државите:

Врз основа на едноставна анализа, плус напорите на Кнут, можеме да го кажеме следново:

Сите турнеи мора да започнат или да завршуваат во Мејн, бидејќи Мејн има само еден сосед. Ние ќе го користиме Мејн како почетна точка.
Сите патувања мора да завршат над Newујорк, бидејќи тоа е точка на артикулација.
Има вкупно 68,656,026 различни капитални патувања.

Ова е најкратката турнеја со капитал, во вкупна вредност од 11,698 милји:

Ова е најдолгата турнеја со капитал, во вкупна вредност од 18,040 милји:

Боење на графикони

Друга интересна класа на проблеми вклучува боење на мапата. Правило е дека ниту една соседна држава не може да има иста боја. Познатиот Теорема на четири бои наведува дека секој планарен график може да биде обоен со најмногу четири бои.

Бидејќи БДД ги шифрира сите можни решенија на Буловата формула, лесно можеме да пресметаме колку решенија има. За боење на графиконите, ги прилагодуваме нашите брои за да ги елиминираме симетрите поради произволното доделување вредности на бојата (4! Симетрични случаи за 4-боја).

За боење на соседните 48 држави, можни се 533,816,322,048 бои. (Ова е 1/2 бројот пријавен од Кнут, бидејќи неговата мапа го вклучува Вашингтон, ДК како 49-та „држава“, и може да се додели на која било од двете бои што не се користат за Мериленд и Вирџинија.) Еве неколку интересни примери за специјални бои:

Избалансирано боење, во кое секоја боја се користи за точно 12 држави. Вакви бои има 12,554,677,864, што е изненадувачки висок 2.4% од сите можни бои.
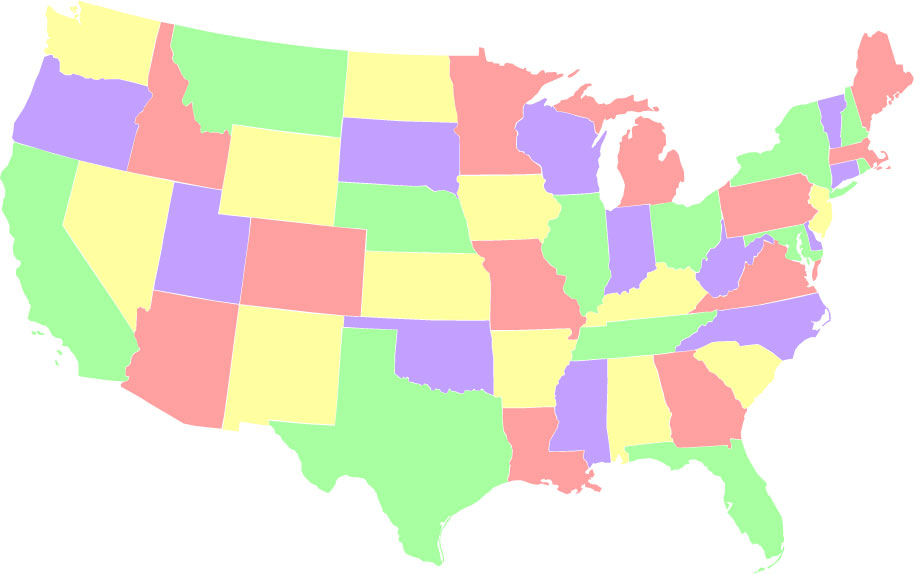
Неизбалансирана боја, во која една од боите (зелена) се користи што е можно помалку (2 состојби). Постојат само 288 начини да се обои мапата така што една боја се користи само двапати.
Небалансирана боја, во која една од боите (жолта) се користи колку што е можно (18 држави). Постојат 71,002,368 начини за боење на картата така што една боја се користи 18 пати.
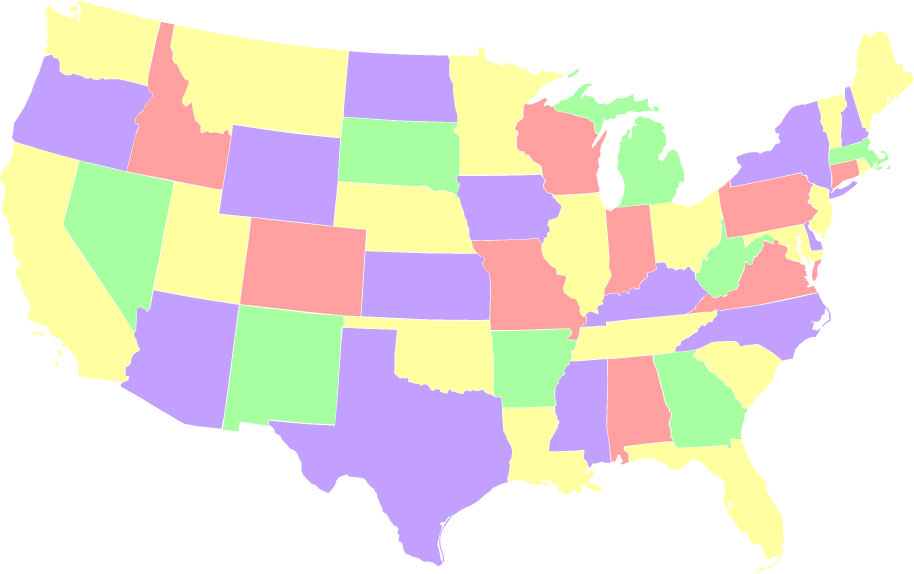
Комбинирање на двете. Бои со употреба на бои 2, 13, 15 и 18 пати. Оваа секвенца 1) од лево кон десно, ја користи секоја боја едноподруго за најмал можен број пати, и 2) од десно кон лево, ја користи секоја боја едноподруго за најмногу можен број пати. Постојат 24 вакви решенија.

Од гледна точка на програми за боење графикони, мапата на 48 држави во САД е прилично едноставна. За повеќе предизвикувачка мапа, видете ја веб-страницата на Мек Грегор График.

Рандал Е. Брајант